I have never seen anything written about this aspect of Bar Modelling. Traditionally, teachers go on courses, train others, and then immediately start to roll out the method to their students. This approach has two problems.
Firstly, the ‘why’ is rarely addressed. In his book, ‘Start with Why’, Simon Sinek explains that the greatest success is experienced by people who understand the rationale behind what they are doing. This is frequently true in mathematics.
Otherwise, the bar method can seem to be adding further complexity to what might already be a complex multi-step problem. (“And now we have to make it even harder by wasting time adding pictures!”)
Secondly, the method of introduction is typically to show children a problem and then explain that you have a pictorial method for solving it. All fine, except for the children who already have, or believe they have, a perfectly adequate method already. To them, this bar seems unnecessary. The damage is done – they will resist and reject, until they find a question so complex that they have no workable method at their disposal, at which point they find themselves overtaken by the children who DID learn the model.
The solution lies in the first step of mastery: pre-teaching. The following tasks, aimed at 5-7 and 7-11 year-olds respectively, address both of the above problems.
1. How Many?
Give pairs of children a dice. Each child should also have a different coloured stick of 6 linking cubes.

Ask both children to roll the dice and make a stick of cubes equal to the number rolled, then put their two sticks together thus:
Finally, a short conversation should take place. Initially the teacher will need to model the language of course, but chil
dren will quickly build their ?uency.
Will: “I have four” Ali: I have two” Will: “Four add two equals six” Ali: “Altogether we have six”.
For 7-11 year-olds, change this slightly. Make a stick of ten cubes, and tell children that each cube is worth the same amount of money. Then tell them that the whole stick is worth, for example, 30p. Ask them how they would find the value of each cube. Here you are looking for “30p divided by 10”, and NOT just ‘3p”. This is important for mastery. Repeat with different values.
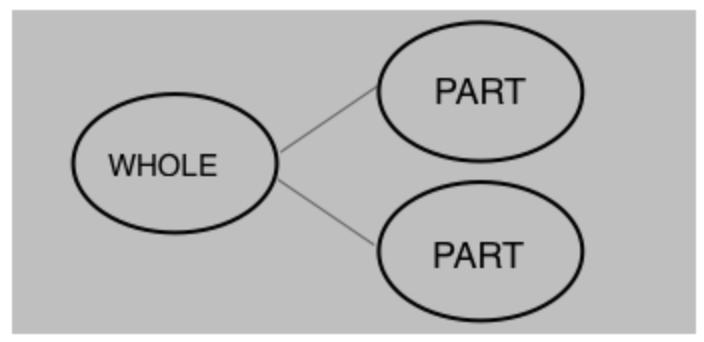
2. Part-Part-Whole
Create this image on an A3 sheet. Put 5 counters into the ‘whole’ section. Invite children to slide the counters into the two ‘parts’ sections. Encourage descriptive discussions such as “We split 5 into (say) 3 and 2. This part is 3 and this part is 2”, or “Three less than 5 is 2,” etc. Repeat with different numbers of counters. For older students, create a similar image but with the whole split into three parts. In stages 3-6, change the discussion to fractions, for example: “I have and you have and altogether we have which is the whole.”
3. More or Less
Group children into threes. Each rolls a dice and uses the number to create a bar of cubes, for example:
Next they compare their quantities using ‘more’, ‘fewer’ or ‘less’ . For example, they might say “The yellow bar has two more cubes than the red bar.”, or “The red bar has three fewer cubes than the blue rod.” For older children, introduce the word difference: “The difference between the red bar and the blue bar is three cubes.”
4. Draw Me
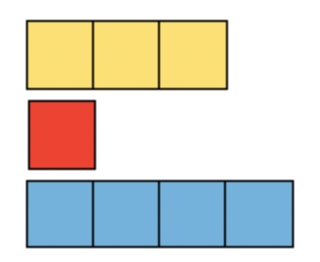
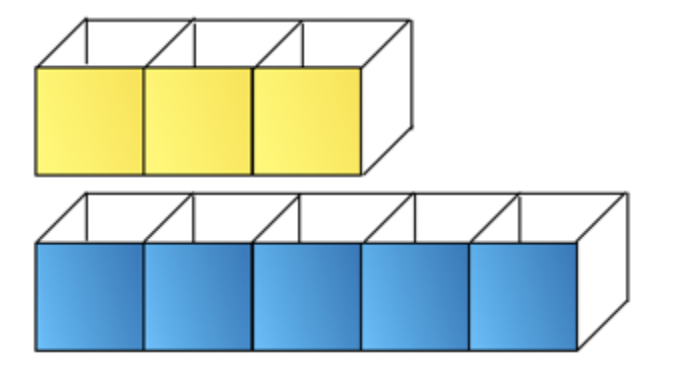
Ask children to draw out on paper the bars that they made in the earlier tasks. This step is often missed, leading to too abstract a jump in children’s minds. For older children, I recommend a task entitled ‘Bar Modelling backwards’, which works as follows. Display an image such as this one and ask questions about it, rather than extrapolate from a word problem. This strips away all context, allowing them to focus purely on the bars’ structure.
Questions you might ask include:
“If there are 3 apples in each box, how can we find out the number of apples in the yellow bar?” As before, do not accept “9 apples” as an answer.
“If there are 20 apples in the blue bar, how can we find out how many apples are in each box?”
“If there are 8 more apples in the blue bar than the yellow bar, how can we find out how many apples are in the yellow bar?”
Each of these ‘how can we find out’ questions forces children to think about the structure of the diagram, rather than just calling out a number, and so learn to master the techniques involved in bar modelling. Vary the numbers involved, until all children are capable of answering.
Further Reading
Sinek, S., 2011. Start With Why. Penguin Books Ltd.
Jeffrey, A. 2019 Bar Modelling Book 1. Macmillan Education Ltd.
Jeffrey, A. 2019 Bar Modelling Book 2. Macmillan Education Ltd.